Matematyka (z łac. mathematicus, od gr. μαθηματικός mathēmatikós, od μαθηματ-, μαθημα mathēmat-, mathēma, „nauka, lekcja, poznanie”, od μανθάνειν manthánein, „uczyć się, dowiedzieć”; prawd. spokr. z goc. mundon, „baczyć, uważać”) – nauka dostarczająca narzędzi do otrzymywania ścisłych wniosków z przyjętych założeń, zatem dotycząca prawidłowości rozumowania. Ponieważ ścisłe założenia mogą dotyczyć najróżniejszych dziedzin myśli ludzkiej, a muszą być czynione w naukach ścisłych, technice a nawet w naukach humanistycznych, zakres matematyki jest szeroki i stale się powiększa.

GRUPA MEDIA INFORMACYJNE & ADAM NAWARA

CIEKAWOSTKI O LICZBACH

Liczby pierwsze

Liczby doskonałe

Liczby bliźniacze

Liczby zaprzyjaźnione

Liczba złota

Liczby względnie pierwsze

Liczby palindronomiczne

Liczby lustrzane

Liczby trójkątne

Liczby kwadratowe

Liczby Fermata

Liczba pierwsza to liczba naturalna, podzielna tylko przez 1 i samą siebie. Liczby 0 i 1 nie są zaliczane do liczb pierwszych, ani do złożonych.

Liczb pierwszych jest nieskończenie wiele. Twierdzenie to udowodnił w IV w. p.n.e. matematyk grecki Euklides.  Aby znależć kolejne liczby pierwsze można posłużyć się metodą zwaną sitem Eratostenesa.  Wypisuje się kolejno liczby naturalne od 2 do n. Liczba 2, pierwsza z wypisanych liczb, jest liczbą pierwszą; pozostawia się ją i wykreśla się wszystkie dalsze liczby podzielne przez 2, gdyż nie są to liczby pierwsze.  Z liczb pozostałych po tym wykreśleniu kolejną po liczbie 2 jest liczba 3. Pozostawia się ją jako liczbę pierwszą  i wykreśla się wszystkie dalsze liczby podzielne przez 3, które nie zostały poprzednio wykreślone. Z pozostałych teraz liczb kolejną po 2 i 3 jest liczba 5; pozostawia się ją i wykreśla wszystkie dalsze liczby podzielne przez 5, które nie zostały dotychczas wykreślone. Kontynuując to wykreślanie, dojdzie się wreszcie do tego, że wszystkie liczby, które nie są pierwsze zostaną wykreślone, pozostaną tylko liczby pierwsze nie większe od n.  Obecnie za pomocą super szybkich komputerów można znaleźć gigantyczne liczby pierwsze.

Ciekawostki:

- Liczba pierwsza 2^6972593-1 (odkryta 1 czerwca 1999 roku) ma ponad 2 mln cyfr, dokładnie 2 098 960. Jest ona 38 z kolei tzw. liczbą Mersenne'a. 

- Największą znalezioną dotąd liczbą pierwszą jest liczba: 2^13466917-1. Rekordzistkę odkryto 14 listopada 2001 roku. Liczba ta składa się z 4053946 cyfr! Co więcej, liczba ta należy do tzw. liczb Mersenne'a (jest to 39 liczba pierwsza Mersenne'a). Odkrycie zostało dokonane w ramach wspomnianego wyżej programu GIMPS, w którym obliczeń dokonują wspólnie pracujące w Internecie komputery ponad 130 tysięcy badaczy-ochotników, zaprzęgając do poszukiwań ponad 200 tysięcy komputerów PC.

- Liczba 11111111111111111111111 złożona z 23 jedynek jest pierwsza.

- Istnieją liczby pierwsze złożone z kolejnych cyfr np.: 23, 67, 4567, 23456789, 1234567891, 1234567891234567891234567891. W dwóch ostatnich liczbach cyfry występują w tak zwanym rosnącym porządku cyklicznym, tzn. po kolei, z tym że po 9 może być 0 lub 1. Trudniej trafić na liczby pierwsze z malejącym porządkiem cyklicznym: 43, 10987, 76543 i 1987.

- liczba 31415926535897932384626433832795028841 zestawiona z początkowych 38 cyfr rozwinięcia dziesiętnego liczby π, jest pierwsza.

- Liczba 73939133 nie tylko jest pierwsza, ale liczby otrzymane z niej przez kolejne obcinanie cyfr od prawej też są pierwsze: 7393913, 739391, 73939, 7393, 739, 73, 7.

Liczby doskonałe

Liczba doskonała to taka liczba naturalna, która jest równa sumie wszystkich swoich dzielników mniejszych od niej samej. Liczby doskonałe zostały wynalezione przez pitagorejczyków. To oni podali pierwsze cztery kolejne liczby doskonałe: 6, 28, 496, 8128 (np. 6=1+2+3, 28=1+2+4+7+14). Nie wiadomo, czy istnieje nieskończenie wiele liczb doskonałych. Nie wiadomo również, czy istnieje choć jedna liczba doskonała nieparzysta. Zagadnieniem liczb doskonałych zajmował się Euklides (IV w. p.n.e.). Podał on regułę odnajdowania parzystych liczb doskonałych:

N=2^k-1(2^k-1),

gdzie (2^k-1) musi być liczbą pierwszą dla k>1 (naturalnego). Liczbami  doskonałymi są również liczby: 2^{23 208}(2^{23 209}-1), 2^{44 496}(2^{44 497}-1). Druga z nich ma w zapisie dziesiętnym ponad 50 tys. cyfr.  W roku 1952 po raz pierwszy użyto do poszukiwań  maszyny liczącej. Do tego roku znano ich tylko 12, w ciągu roku znaleziono kolejne 5. W 2001 roku znaleziono 39-tą liczbę doskonałą.

Ciekawostki:

- Liczba doskonała: 2^6972592(2^6972593-1) ma 4 197 919 cyfr. Odkryto ją 1 czerwca 1999 roku.

- Największa znaleziona dotąd liczb doskonała to: 2^13466916(2^13466917-1).  

Liczby bliźniacze

Liczbami bliźniaczymi nazywamy dwie liczby pierwsze różniące się o 2. Liczbami bliźniaczymi są więc np. następujące pary liczb: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), ... Nie wiadomo do chwili obecnej, czy istnieje nieskończenie wiele par liczb bliźniaczych. 

Dwie liczby A i B nazywają się zaprzyjaźnionymi jeżeli suma wszystkich dzielników liczby A (mniejszych od niej samej) jest równa liczbie B i odwrotnie, suma wszystkich dzielników liczby B (mniejszych od niej samej) jest równa liczbie A. Takimi liczbami "przyjaciółkami" są liczby jak wykazał Pitagoras: 220 i 284. Istotnie, 220=1+2+4+71+142, a więc liczba 220 jest sumą dzielników liczby 284, a 284=1+2+4+5+10+11+20+22+44+55+110, a więc liczba 284 jest sumą dzielników liczby 220. Każda liczba doskonała jest zaprzyjaźniona sama ze sobą. Znanych jest około miliona par liczb zaprzyjaźnionych. Nie wiadomo jednak czy istnieje ich nieskończenie wiele. Poniższa tabela podaje 10 przykładów par liczb zaprzyjaźnionych: 

Ciekawostki:

- Na początku 2001 roku Mariano Garcia znalazł milionową parę liczb zaprzyjaźnionych.  W maju 2001 roku znaleziono już aż 2122263 pary takich liczb.
- Liczby zaprzyjaźnione znane były już w szkole Pitagorasa (VI w.p.n.e), przypisywano im znaczenie mistyczne. Starożytni Grecy wierzyli, że amulety z wygrawerowanymi liczbami zaprzyjaźnionymi zapewniają szczęście w miłości.                                            

Liczba złota

Liczba złota liczba charakteryzująca złoty podział odcinka jest równa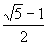 
Kolejne przybliżenia liczby złotej można otrzymać obliczając ilorazy sąsiednich liczb Fibonacciego czyli liczb: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... Ilorazy te są równe: 0, 1, 1/2, 2/3, 3/5, 5/8, 8/13, 21/34, 34/55, 55/89... Jako pierwszy wyrysował złoty podział Hippasus w V wieku p.n.e. Starożytni Grecy uważali złoty podział za idealną proporcję, którą chętnie realizowali w architekturze. Wielki astronom Kepler powiedział:

"Geometria ma dwa cenne skarby: jeden z nich to twierdzenie Pitagorasa, drugi - podział odcinka w stosunku średnim i skrajnym. Pierwsze porównać do miary złota. Drugie jest niby kamień drogocenny".

Obecnie złoty podział jest też często stosowany, np. wymiary znormalizowanego zeszytu pozostają w stosunku w przybliżeniu równym stosunkowi złotego podziału.

Liczba złota ma ciekawe własności:

- aby ją podnieść do kwadratu, wystarczy dodać do niej jedynkę,
- aby znaleźć jej odwrotność, wystarczy odjąć jedynkę.

Liczby względnie pierwsze

Liczby, które nie mają wspólnego dzielnika nazywamy liczbami względnie pierwszymi. Parą liczb względnie pierwszych jest licznik i mianownik ułamka nieskracalnego, np. 6 i 13 . Liczby te mają następujące własności: ich najmniejsza wspólna wielokrotność jest równa ich iloczynowi

- jeśli liczba b jest liczbą względnie pierwszą względem każdej z liczb c,d,e,f,..., to jest także względnie - pierwsza względem iloczynu tych liczb

Liczby palindromiczne

Liczbę naturalną, którą czyta się tak samo od początku i od końca nazywamy palindromem. Przykłady liczb palindromicznych: 55, 494, 30703, 414, 5115..

Liczby lustrzane

Liczby lustrzane to takie dwie liczby, które są lustrzanym odbiciem, np.: 125 i 521, 68 i 86, 3245 i 5423, 17 i 71. Jeżeli napiszemy dowolną liczbę i jej lustrzane odbicie , np.1221, to tak otrzymana liczba jest podzielna przez 11, np. 1221:11=192.

Liczby trójkątne

Liczby postaci 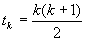  , gdzie k jest liczbą naturalną. Liczba  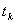jest sumą k kolejnych liczb naturalnych. Nazwa liczby trójkątne pochodzi stąd, że 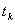 jest liczbą kół jednakowej wielkości, z których można utworzyć trójkąt równoboczny o boku zbudowanym z k kół. Przykłady liczb trójkątnych: t₁=1, t₂=3, t₃=6, t₄=10.

Liczby kwadratowe

Nazwa "liczby kwadratowe" pochodzi stąd, że każda taka liczba  o numerze n jest liczbą np. kół jednakowej wielkości, z których można ułożyć kwadrat o boku  zbudowanym z n kół.

Liczby Fermata

Liczby Fermata  to liczby mające postać 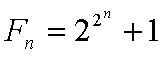, gdzie n jest liczbą całkowitą większą lub równą zero. Początkowo sądzono, że wszystkie tego typu liczby są pierwsze.  Liczby F₀=3, F₁=5, F₂=17, F₃=257, F₄=65537 są liczbami pierwszymi, jednak  F₅=4294967297 jest liczbą złożoną podzielną przez 641. Nie wiadomo, czy istnieją inne liczby pierwsze, które są jednocześnie liczbami Fermata.